Symbolic Solver

The below is copied from my post over at julia discourse.

August 2024

A new symbolic solver authored by me has just been merged to Symbolics.jl, and is available in the latest release (v6.2.0). I want to share some of its capabilities here!

Link to PR

The solver features:

Multivariate polynomial solving
Exact (symbolic) solutions
Solving using isolation and attraction (inspired by a paper from R. W. Hamming)

Examples and usage!

Solving with parameters and transcendental functions:

            julia> @variables a b c d e x;
            
            julia> symbolic_solve(a*log(x)^b + c ~ 0, x)
            1-element Vector{SymbolicUtils.BasicSymbolic{Real}}:
             e^((-c) / a)^(1 / b))
        

Solving by detecting polynomialization opportunities (\(9^x + 3^x = 0\) and the like also works)

        julia> symbolic_solve(sin(x^2 +1)^2 + sin(x^2 +1) + 3)
        [ Info: var"##426" ϵ Ζ
        [ Info: var"##429" ϵ Ζ
        4-element Vector{SymbolicUtils.BasicSymbolic{Complex{Real}}}:
         (1//2)*√(-4(1 - asin((1//2)*(-1 + (0 + 1im)*√(11))) - (π*2var"##426")))
         (-1//2)*√(-4(1 - asin((1//2)*(-1 + (0 + 1im)*√(11))) - (π*2var"##426")))
         (1//2)*√(-4(1 - asin((1//2)*(-1 - ((0 + 1im)*√(11)))) - (π*2var"##429")))
         (-1//2)*√(-4(1 - asin((1//2)*(-1 - ((0 + 1im)*√(11)))) - (π*2var"##429")))
    

Solving high degree polynomials exactly:

        julia> expr = expand((x + 2)*(x^2 + 2x + 1)*(x^4 - 3x^3 + x + 5)*(x^4 - 1))
        -10 - 27x - 25(x^2) - 3(x^3) + 22(x^4) + 34(x^5) + 24(x^6) + 2(x^7) - 12(x^8) - 7(x^9) + x^10 + x^11
        # output is truncated
        julia> symbolic_solve(expr, x, dropmultiplicity=false)
        9-element Vector{Any}:
        -2
        -1
        ...
        (-1//2)*(0 + 2im)
    

Also works with parameters:

        julia> expr = expand((x + b)*(x^2 + 2x + 1)*(x^2 - a))
        -a*b - a*x - 2a*b*x - 2a*(x^2) + b*(x^2) + x^3 - a*b*(x^2) - a*(x^3) + 2b*(x^3) + 2(x^4) + b*(x^4) + x^5
        julia> symbolic_solve(expr, x, dropmultiplicity=false)
        5-element Vector{Any}:
        -1
        -1
        -b
        (1//2)*√(4a)
        (-1//2)*√(4a)
        

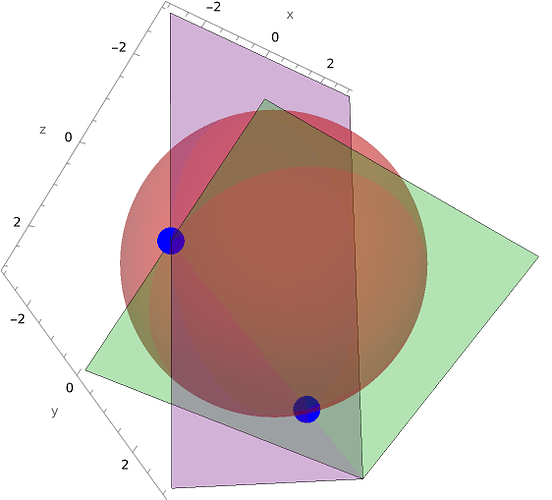
Exact intersection of a sphere and a line in \(\mathbb{C}^3\):

            julia> symbolic_solve(
               [x^2 + y^2 + z^2 - 9, 
               x - 2y + 3,
               y - z]
               ,[x,y,z])
            2-element Vector{Any}:
            Dict{Num, Any}(z => 2, y => 2, x => 1)
            Dict{Num, Any}(z => 0, y => 0, x => -3)
        

For the example above, we can check our answers by plotting everything. As expected there are only 2 intersections with the same coordinates our solver found:

System of polynomials with infinite solutions are solved in terms of one of the variables:

            julia> symbolic_solve([x*z - y - 1, x + z], [x, y, z])
            ┌ Warning: Infinite number of solutions
            └ @ SymbolicsGroebnerExt ~/code/julia/Symbolics.jl/ext/SymbolicsGroebnerExt.jl:216
            1-element Vector{Dict{Num, Any}}:
            Dict(z => z, y => -1 - (z^2), x => -z)
        

Note and credits

Many thanks to alex and shashi for being great mentors throughout the project’s length!